数学教学中学生创新能力的培养
大庆市第三十七中学数学教师  林守义
   

      “一个民族没有创造，就没有希望；一个国家没有创造，就没有前途。”以信息社会和市场经济为基本形态的21世纪，科学技术迅猛发展，现代数学渗透到各个领域。因此，数学教学应着重培养学生的创新意识和创新能力。
1． 指导学生勇于思索、发现问题。
数学教学中指导学生独立思考，善于发现问题、提出问题，是培养学生创新能力的一个重要途径。如学习直线公理后，有这样一道思考题：平面内有n个点，共中任意三点不共线，过其中两点画直线，一共可以画多少条直线？有些学生感觉无从下手，没有思路。教师如果这样指导：过平面内不共线三点中的两点可以画多少条直线？四点呢？五点呢？六点呢？……n点呢？学生经过探索、思考后发现其规律是：直线总条数等于1+2+……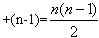，当学生自己发现、总结出这个规律之后，就会迎刃而解发下三个问题：
（1）平面内n条直线两两相交，最多有多少个交点？
（2）直线1上有n个点，有多少条不同的线段？
（3）从∠AOB的项点在其内部引出（n-2）条射线，共有多少个不同的角
2．发挥学生主体作用，精讲精练。
 充分调动、激发学生的积极性、主动性，引导、鼓励学生主动去观察、探索，力求通过学生自己的思考去获得知识，这是培养学生创新能力的一项长期工作。在分式第一节课中，通过学生阅读、讨论，归纳出本节的主要内容：
① 分式的概念；②有理式包括整式和分式；③三种基本题型。
做完书中练习后，教师只讲三句话：①我们现在判断一个代数式是否是分式，主要看分母是否含有这母，但不能说分母里含有字母的式子叫分式。这在第十一章会学到；②分式和分数有很多类似的性质，今后对比学习；③分式的值为零是一种什么情况？学生思考后，便知是分母为零，分式我意义。立刻给学生出这样一道练习题：
当且仅当x=-1时分式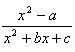 的值为零，当x=3时分式无意义。求：a、b、c的值。本来是一道不简单的题，学生经过积极思考，能独立完成。45分钟的课教师只讲5、6分钟，其余的时间敢于放手让他们去尝试、去探索，自己主动获得知识，而不是被动接受。
3．培养学生自学能力，学会会学。
一个人的一生需要不断学习，才能适应社会不断变化、不断进步的需要。因此，数学教育在传授知识的同时，必须使学生具备丰富自己知识的能力。这是创新能力的前提。
学生通过画图可知：两条直线被第三条直线所截，同位角相等，两直线平行。这是两直线平行的判断公理，（引导）提问：两条直线被第三条直线所截，除同位角外，还有内错角和同旁内角，他们能否满足一定的条件也能得到两直线平行呢？学生迫不急待的阅读课本，不但掌握内错角和同旁内角需满足的条件，而且知道满足的条件应推出同位角相等，进而两直线平行。整节内容主要是由学生阅读课本，自学得到的。
4．牢固掌握基础知识，提高能力。
学生掌握必要的基础知识，是培养创新能力的基础。数学概念、公式、法则、方法，学生不但要理解、掌握，还要灵活运用，分析、解决问题。
（1）变式练习既能使学生理解加深、掌握所学知识，又能培养学生分析和解决问题的能力。
例1：不等式 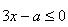只有三个正整数解，求a的取值范围。
变1：不等式 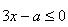只有三个正整数解，求正整数a的值。
变2：不等式 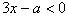只有三个正整数解，求a的取值范围。
 学生自编题1：不等式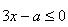 只有两个（或四个、五个…）正整数解，求 a的取值范围。
 学生自编题2：不等式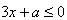 只有三个正整数解，求a 的取值范围。
学生自编题3：不等式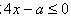 只有三个正整数解，求a的取值范围。
学生自编题4：不等式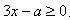 只有三个正整数解，求a 的取值范围。
……
 学生还会自编出与本题型类似的许多题目，这样不但培养学生的探索能力、应变能力，而且更能培养学生的创造能力。
 （2）开拓解题思路，培养发散思维能力。
指导学生从不同方面、不同角度去分析问题，就能找出不同的解题途径。
 例2：一件工程要在计划时间内完成，若甲单干正好完成，若乙单干能超过计划6天完成，现甲、乙合作4天以后，余下的乙单干，正好按计划日期完成。
问：计划日期是几天？
解：设计划日期是x天。
由题意得：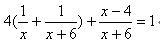
解完后让学生继续思考，讨论还有哪些解法？易得到：
列法②：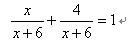
列法③：
 这样可以打破学生常规思维，培养发散思维。为学生的发明、创造奠定思维基础。
 （3）运用类比思想，有助于发现创新，解决问题。
 奥地利医生奥恩布鲁格，曾将积有脓水的胸腔和盛了酒的酒桶进行类比，根据敲酒桶可以知道里面是否有酒，从而推知敲胸腔也可以知道里面是否有脓水，在这一类比结论的基础上，他发明了“叩诊法”。数学教学中，通过类比，可以从中受到启发，从而顺利地解决新的问题。
 例3：解方程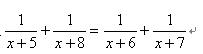
通过类比可以容易解决如下问题。
例3’：解分式方程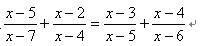
例3’’：解分式方程
       总之，“积极实行启发式和讨论式教学，激发学生独立思考和创新的意识，切实提高教学质量。要让学生感受、理解知识产生和发展的过程，培养学生的科学精神和创新思维习惯，重视培养学生收集处理信息的能力、获取新知识的能力、分析和解决问题的能力。